Riješite Kakuro zagonetke

U ovom vodiču nudimo niz praktičnih savjeta o tome kako riješiti Kakuro zagonetke, s težinom koja se kreće od početničke do stručne razine.

Ukratko, pravila: Kakuro je igra zagonetki na ploči sličnoj križaljci u kojoj se znamenke koriste kako bi se zbrojile do vrijednosti navedenih u 'definicijskim' poljima ploče. Osim toga, unutar svake skupine zbrojeva, svaka znamenka može se pojaviti najviše jednom.

Tradicionalni način rješavanja Kakuro zagonetke je inkrementalni: korištenjem postojećih informacija na ploči, možete sa sigurnošću pronaći vrijednost određenog polja koje može imati samo jednu moguću vrijednost. Zatim se ta vrijednost popunjava i postupak se ponavlja sve dok se ne otkriju sva polja na ploči.

U nekim situacijama ne postoji određena ćelija uprave koja ima samo jednu mogućnost. U tim slučajevima svaku od mogućnosti treba istražiti zasebno i eliminirati kroz proturječnosti sve dok ne ostane samo jedan način djelovanja.

U nastavku predstavljamo nekoliko metoda za napredak u rješavanju stvarne zagonetke.

Jedinstveni zbrojevi za specifične definicije

Postoje neke definicije koje se mogu riješiti samo na određeni način:

Zbroj 3 (preko dvije ćelije) uvijek će biti 1 + 2.
Zbroj 4 (preko dvije ćelije) uvijek će biti 1 + 3.
Zbroj 17 (preko dvije ćelije) uvijek će biti 8 + 9.
Zbroj 6 (preko tri ćelije) uvijek će biti 1 + 2 + 3.
Zbroj 24 (preko tri polja) uvijek će biti 7 + 8 + 9.

i tako dalje... Obično možete zadržati pokazivač miša na Kakuro mreži iznad broja definicije i pojavit će se alatni opis koji sadrži sve mogućnosti zapisivanja tog zbroja s jedinstvenim znamenkama u broju dostupnih ćelija.

Zbrojevi koji se mogu zapisati na jedinstven način obično su mali ili veliki zbrojevi koji prisiljavaju male/velike znamenke u odgovoru kako bi se postigli.

Jedinstven način pisanja zbroja pomaže, ali imajte na umu da su sve permutacije valjane i još uvijek morate shvatiti koju stvarnu permutaciju koristiti na ploči.

Ograničenja redaka/stupaca

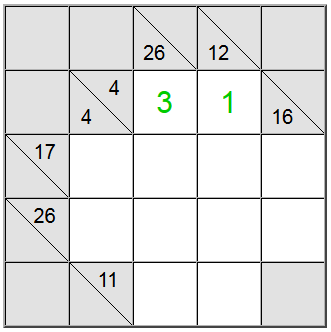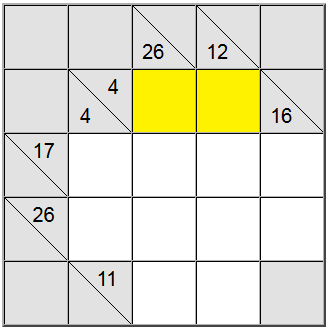
Za gore označene žute ćelije postoji samo jedan način zapisivanja zbroja: 4 = 1 + 3. Međutim, još uvijek moramo shvatiti koju permutaciju (1 + 3 ili 3 + 1) koristiti.

Ispada da nam vertikalna definicija 26 pomaže: zbroj u 4 polja koji bi sadržavao znamenku 1 bio bi najviše 1 + 9 + 8 + 7 = 25. Budući da je naš zbroj 26, ispada da znamenka 1 ne može biti dio zbroja. Stoga je jedini preostali redoslijed za žute kvadrate 3 + 1.

Definicije raskrižja

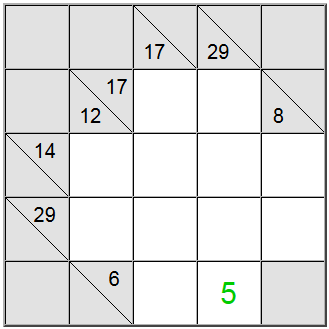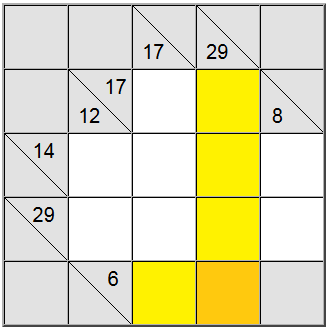
Na gornjoj ploči, horizontalni žuti kvadrati mogu se zapisati kao 6 = 1 + 5 ili 6 = 2 + 4. Vertikalni žuti zbroj može se zapisati samo kao 29 = 5 + 7 + 8 + 9.

Žuti kvadrat pronađen na presjeku te dvije definicije zbroja mora sadržavati istu znamenku, tako da mora postojati zajednička znamenka u horizontalnoj i vertikalnoj definiciji da bi se dijelile. Promatrajući gore navedene mogućnosti, lako možemo zaključiti da je 5 jedina znamenka koja zadovoljava ovaj kriterij.

Ova tehnika posebno dobro funkcionira pri presjecivanju definicije s niskom sumom i definicije s visokom sumom. Definicije s niskom i visokom sumom su one koje imaju relativno nizak ili visok broj definicije sume (6 odnosno 29 za naš primjer) u usporedbi s brojem dostupnih ćelija. Budući da je 6 relativno nizak, prisilit će niske znamenke u prikazu sume, a 29 će prisiliti visoke znamenke (kako bi se postigli ti zbrojevi korištenjem zadanog broja ćelija). Stoga će presjek niskih i visokih znamenki vjerojatno sadržavati samo jednog kandidata za stvarnu vrijednost ćelije.

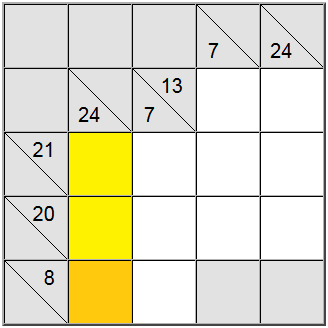
Min. / maks. vrijednosti za grupu zbroja

Ponekad je korisno odrediti maksimalnu ili minimalnu vrijednost za skupinu zbrojeva. To vam može dati osjećaj koji je valjani raspon znamenki za taj određeni zbroj, što će vam zauzvrat pomoći u povezivanju s drugim ograničenjima i određivanju jedinstvenih dodjela na ploči.

U gornjem primjeru, žute okomite ćelije prihvaćaju samo vrijednosti jednake 7 ili više. Ako pokušate dodijeliti 6, lako možete shvatiti da je 6 + 9 + 8 = 23, tako da definicijski zbroj od 24 ne bi bio dostižan.

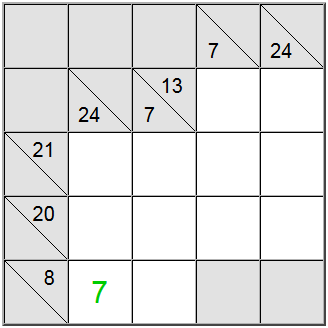
Budući da je 7 minimum, horizontalna definicija s 8 kao zbrojem prisiljava 7 u taj položaj.

Zaključak

Vježbanje je najbolji način da vidite kako se ovaj savjet može primijeniti u stvarnim Kakuro igrama. Zaigrajte zagonetku u stvarnom životu. Želimo vam puno sreće i zabave!

Igraj Kakuro